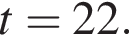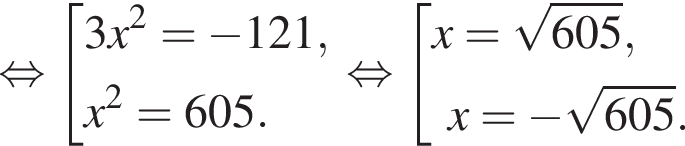Определите наименьшее натуральное число, кратное 2, которое при делении на 11 с остатком дает неполное частное, равное 5.
Выразите 648 см 6 мм в метрах с точностью до сотых.
Сумма всех натуральных делителей числа 50 равна:
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
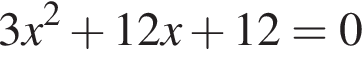
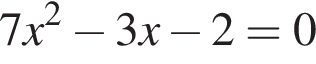
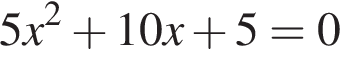
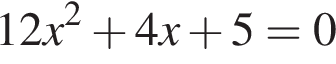
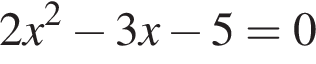
Вычислите 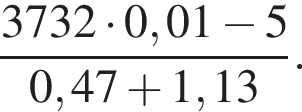
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 127°, ∠BOM = 153°. Найдите величину угла BOC.
Найдите площадь фигуры, изображенной на рисунке.
Вычислите 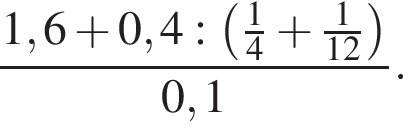
Значение выражения 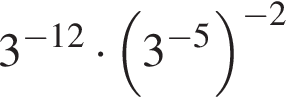 равно:
равно:
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Четырехугольник MNPK, в котором ∠N = 128°, вписан в окружность. Найдите градусную меру угла K.
Упростите выражение 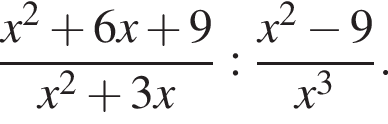
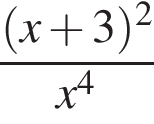
Найдите значение выражения 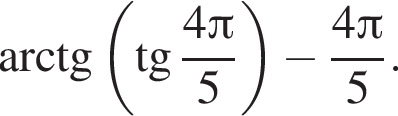
Среди предложенный уравнений укажите номер уравнения, графиком которого является парабола, изображенная на рисунке:
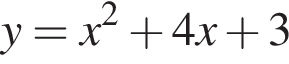
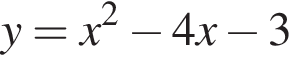
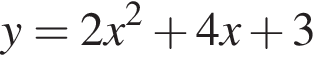
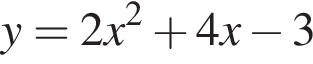
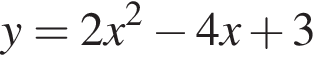
ABCDA1B1C1D1 — куб. Точки M и N — середины ребер B1C1 и CC1 соответственно,
 (см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
(см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
Какая из прямых пересекает график функции 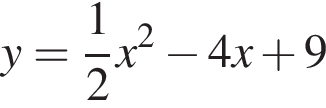 в двух точках?
в двух точках?
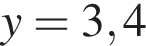
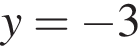

Через точку A высоты SO конуса проведена плоскость, параллельная основанию. Определите, во сколько раз площадь основания конуса больше площади полученного сечения, если SA : AO = 2 : 3.
Корень уравнения
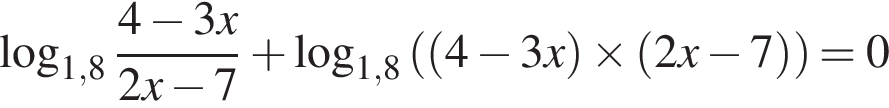
(или сумма корней, если их несколько) принадлежит промежутку:
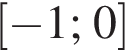
Строительные бригады №1 и №2 купили соответственно 18 и 19 фундаментных блоков у одного из трех поставщиков, выбрав для себя наиболее дешевый вариант. Стоимость одного блока и условия доставки всей покупки приведены в таблице. Определите, на сколько рублей дороже обошлась эта покупка с доставкой одной из бригад. Ответ запишите в рублях.
| Поставщик | Стоимость (тыс. руб. за 1 шт.) | Стоимость доставки (тыс. руб. за всю покупку) | Специальное предложение |
|---|---|---|---|
| 1 | 205 | 1850 | — |
| 2 | 240 | 1950 | Доставка со скидкой 50 %, если сумма заказа превышает 4,5 млн. бел. рублей |
| 3 | 275 | 2050 | Доставка бесплатно, если сумма заказа превышает 5 млн. бел. рублей |
Найдите сумму корней (корень, если он единственный) уравнения 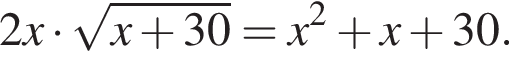
Найдите модуль разности наибольшего и наименьшего корней уравнения 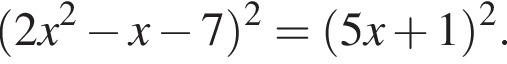
Пусть (x;y) — целочисленное решение системы уравнений
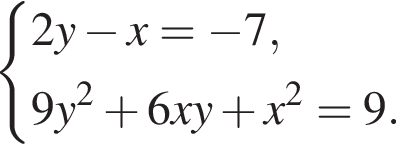
Найдите сумму x+y.
Найдите значение выражения 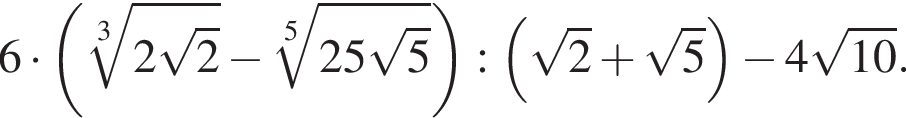
Найдите количество корней уравнения 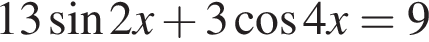 на промежутке
на промежутке 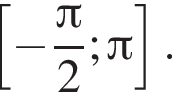
Геометрическая прогрессия со знаменателем 5 содержит 10 членов. Сумма всех членов прогрессии равна 24. Найдите сумму всех членов прогрессии с четными номерами.
Найдите значение выражения: 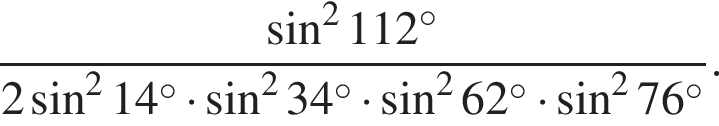
Найдите сумму целых значений x, принадлежащих области определения функции
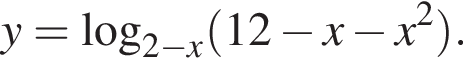
Найдите произведение наименьшего и наибольшего целых решений неравенства 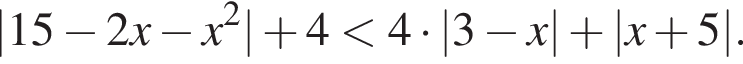
Пусть 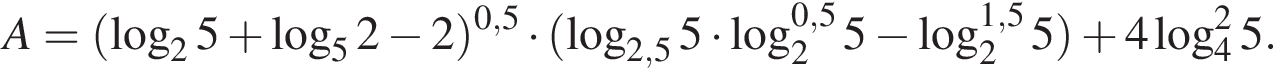
Найдите значение выражения 2A.
Найдите произведение корней уравнения 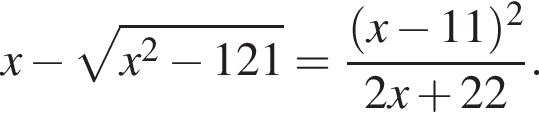

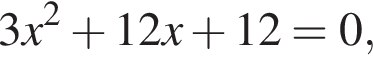 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.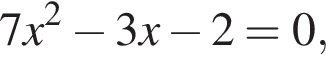 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.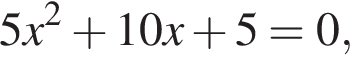 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.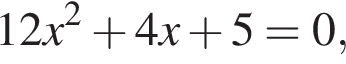 дискриминант меньше нуля, значит, корней нет.
дискриминант меньше нуля, значит, корней нет.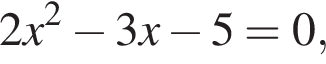 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.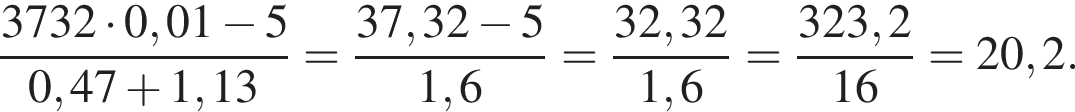
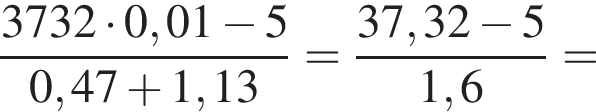
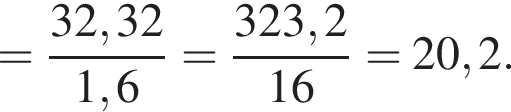
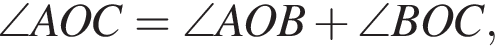
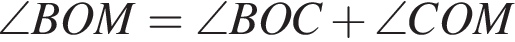 и
и  Таким образом:
Таким образом:
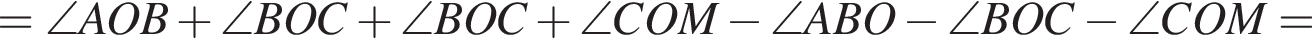
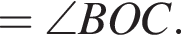

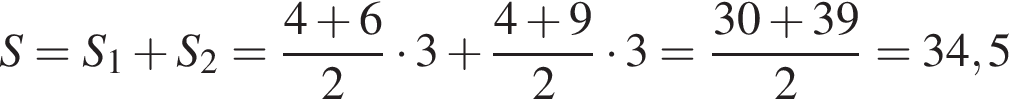
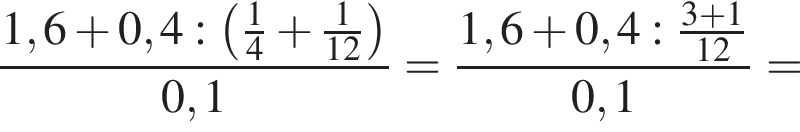
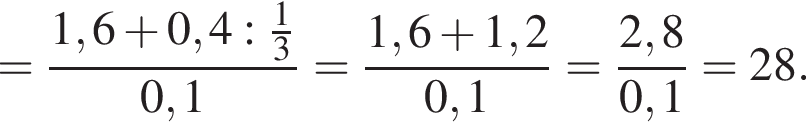
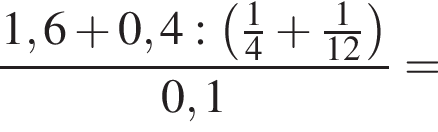
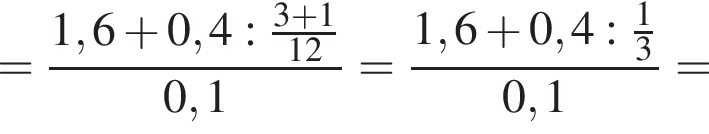
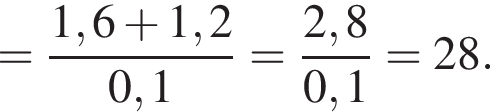
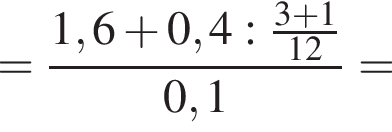
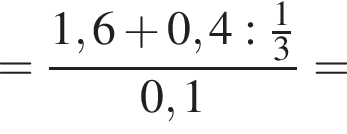
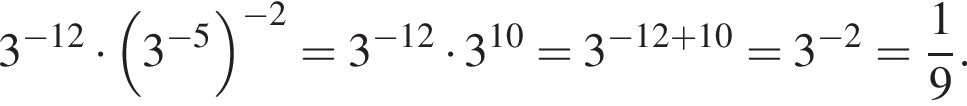
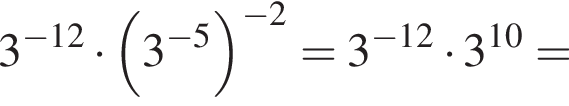
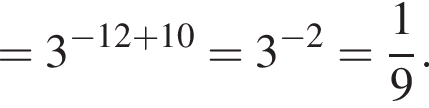


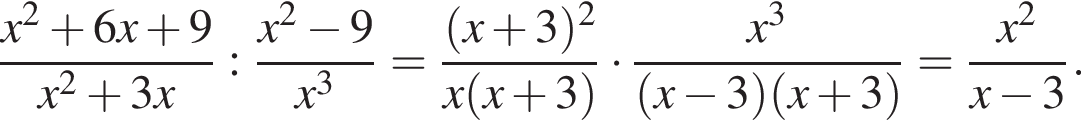
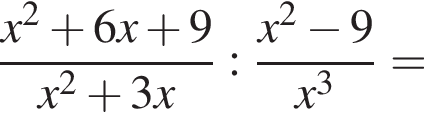
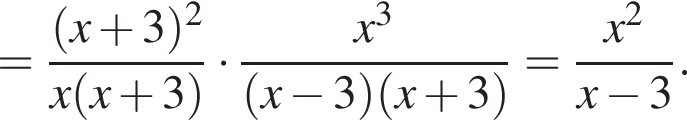
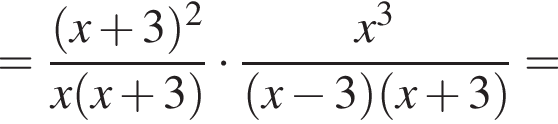
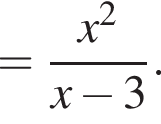
 только для
только для 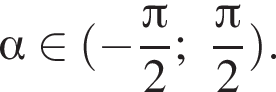 Поэтому преобразуем, используя формулы приведения:
Поэтому преобразуем, используя формулы приведения: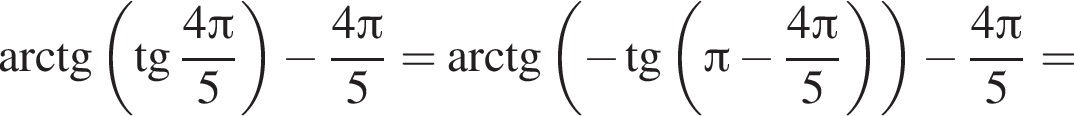
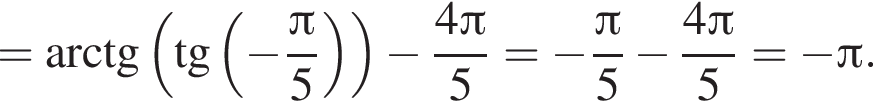
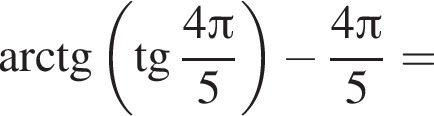
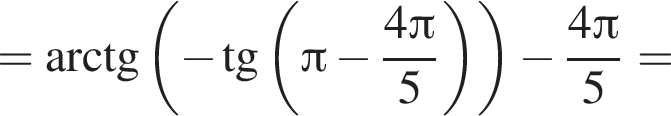
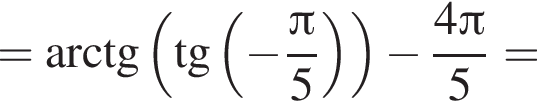
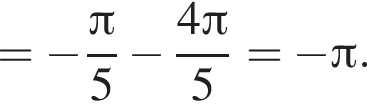
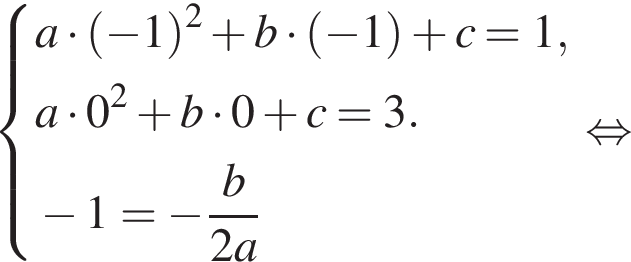
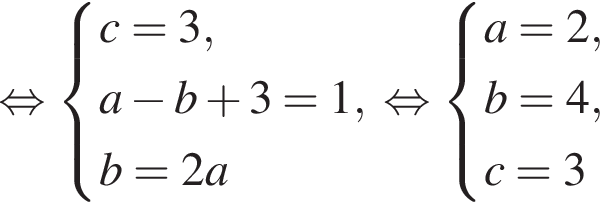
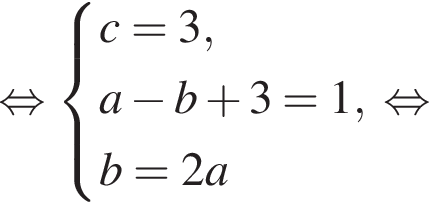
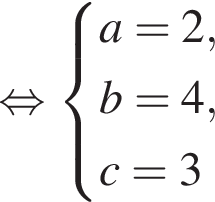
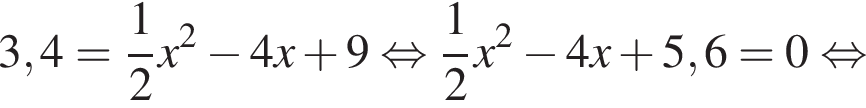
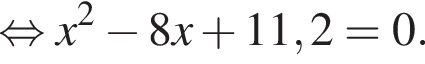
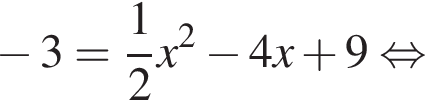
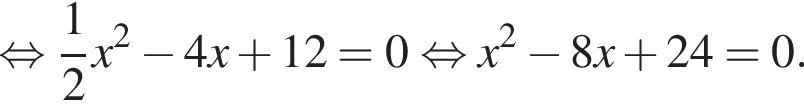
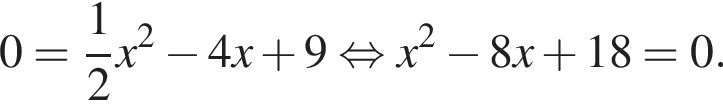 Дискриминант меньше нуля, поэтому пересечений нет.
Дискриминант меньше нуля, поэтому пересечений нет.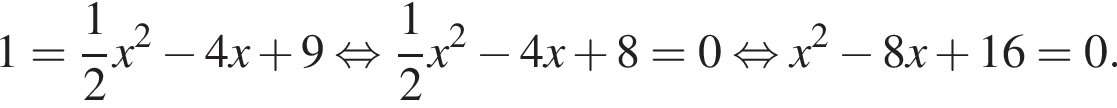
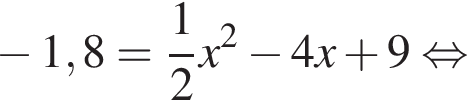
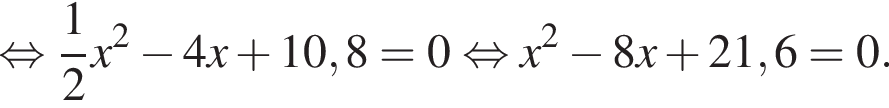
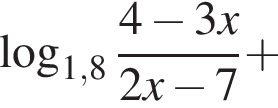
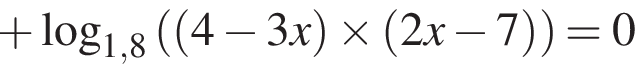
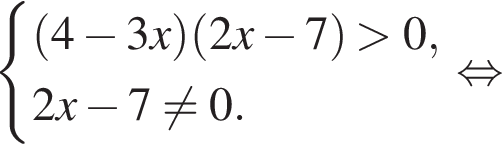
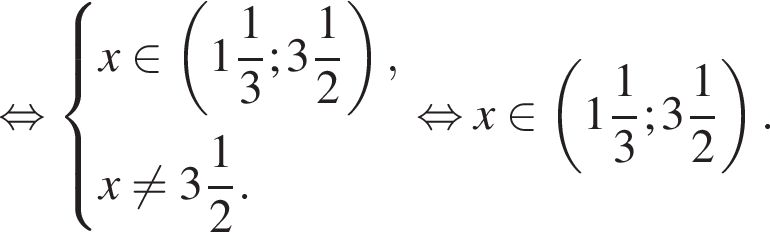
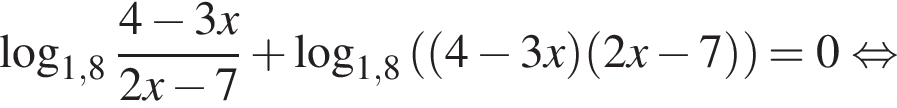
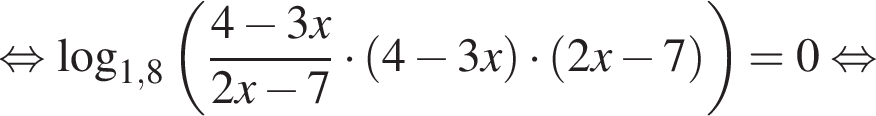
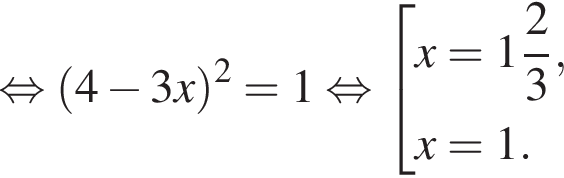
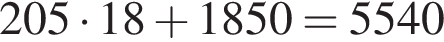 тыс. руб.
тыс. руб.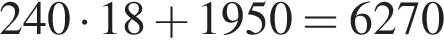 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. Тогда:
Тогда: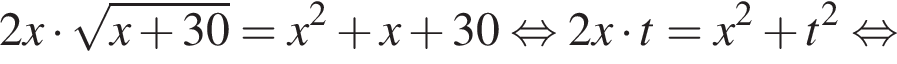

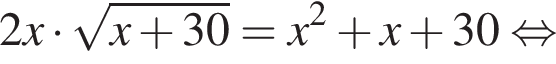


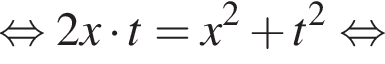
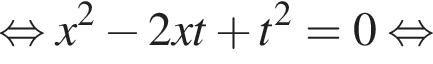
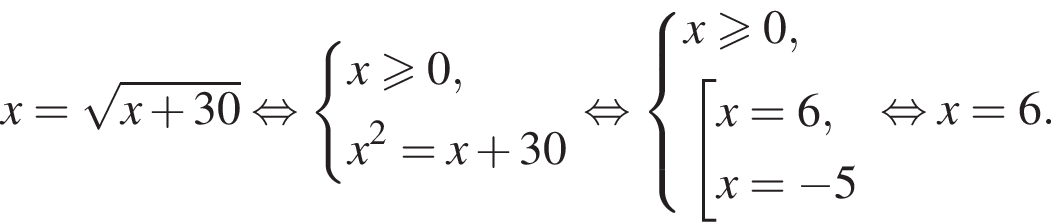
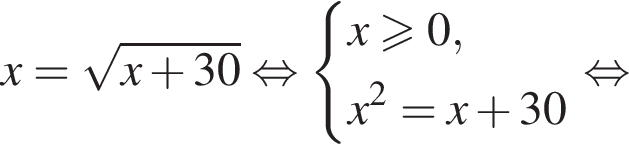
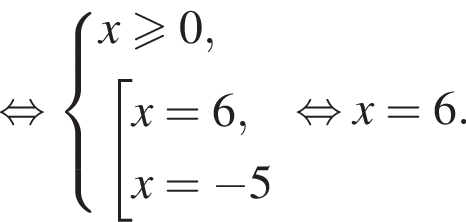
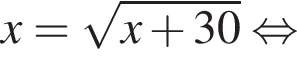
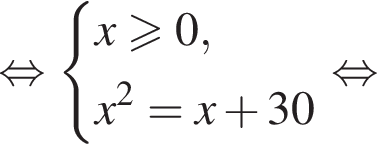
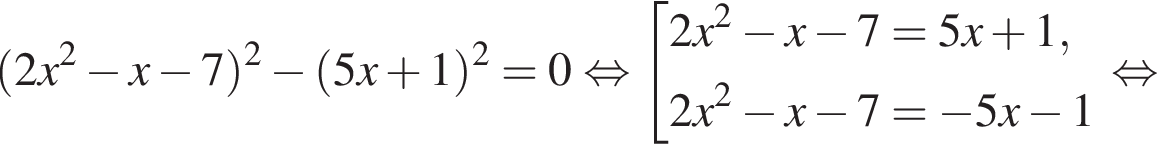
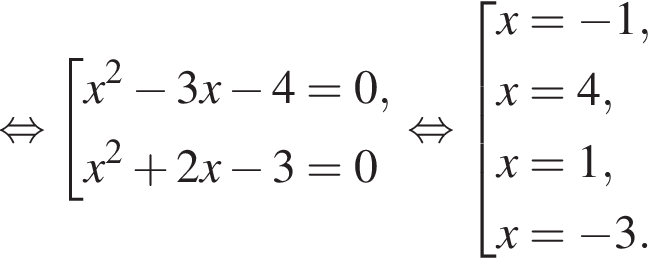
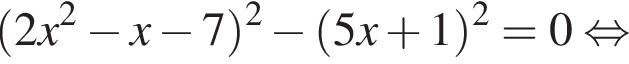
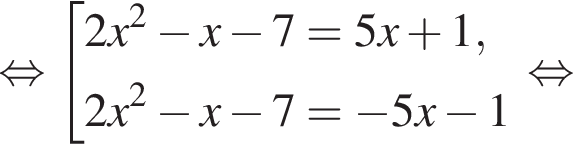
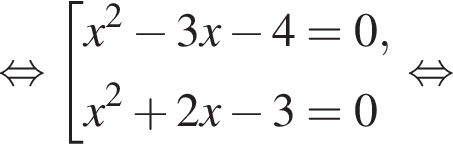
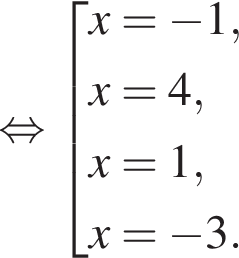
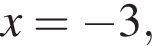 модуль разности наибольшего и наименьшего корней уравнения равен 7.
модуль разности наибольшего и наименьшего корней уравнения равен 7.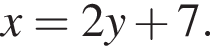 Заметим, что
Заметим, что 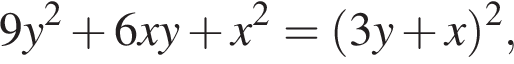 поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим:
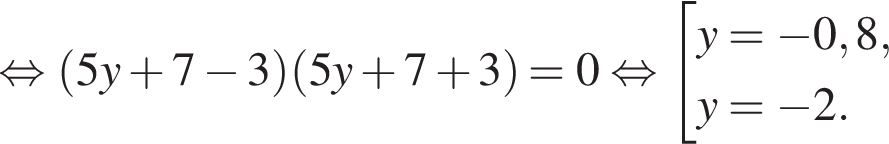
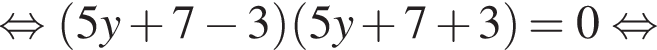
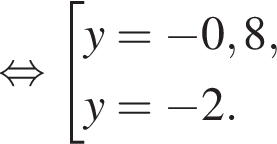
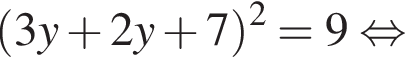
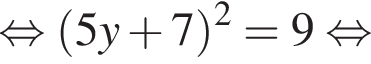
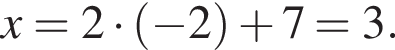 Сумма x+y равна:
Сумма x+y равна: 
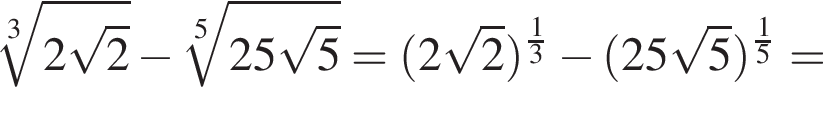
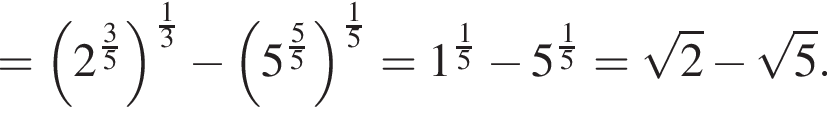
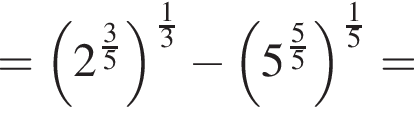
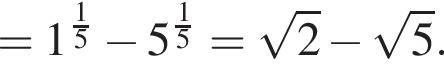
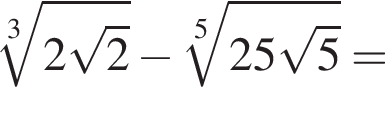
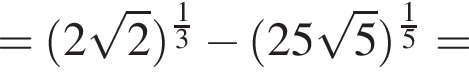
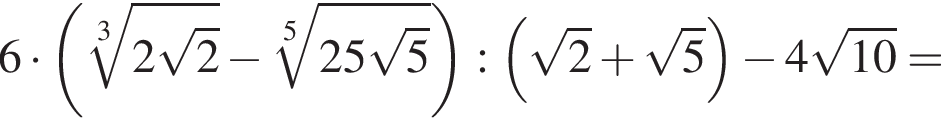
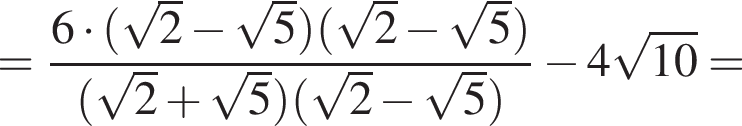
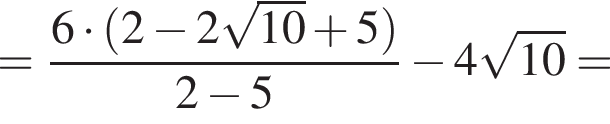

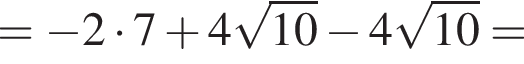
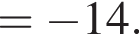
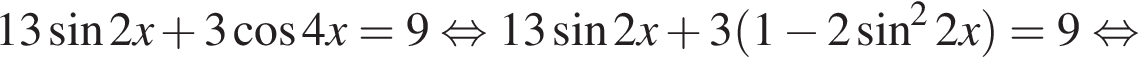

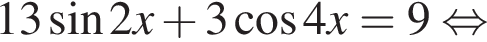
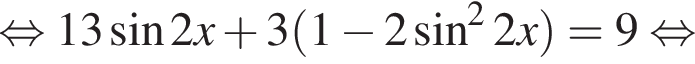
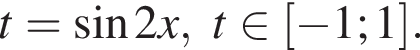 Тогда:
Тогда: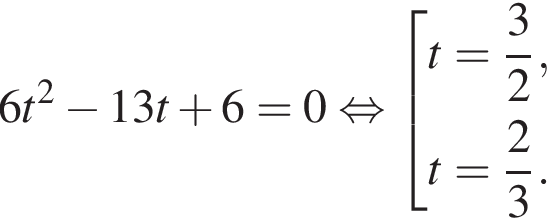
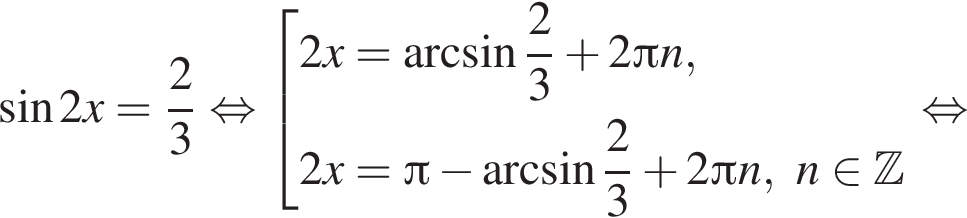
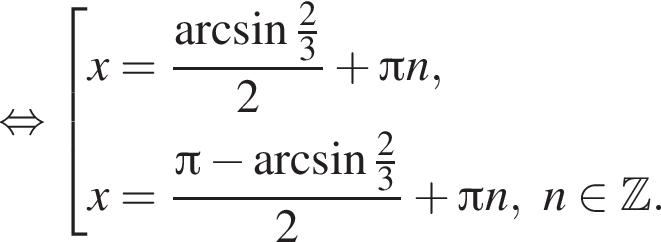
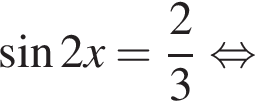
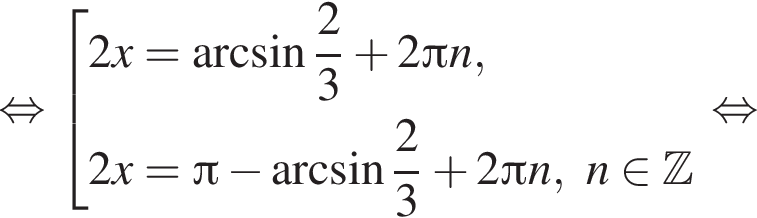
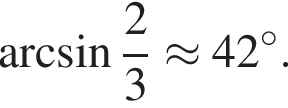 Рассмотрим значения x при различных значениях n:
Рассмотрим значения x при различных значениях n: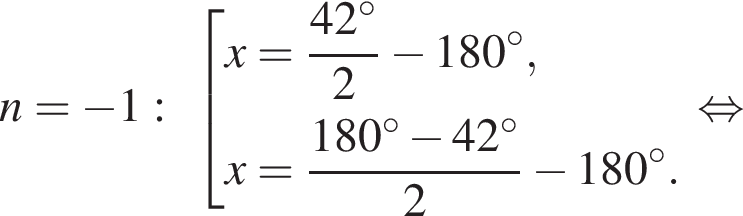
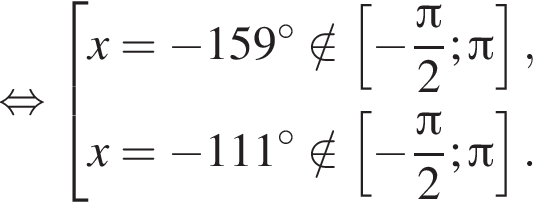
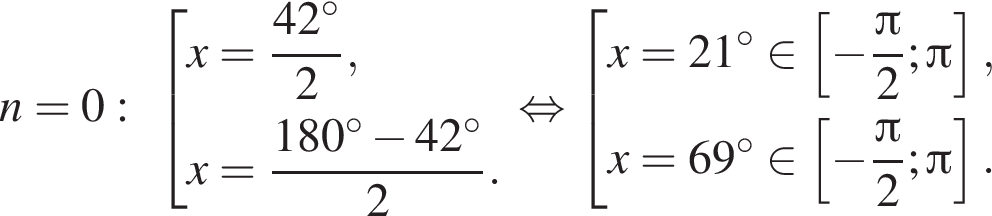
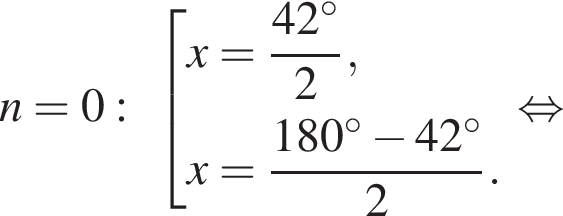
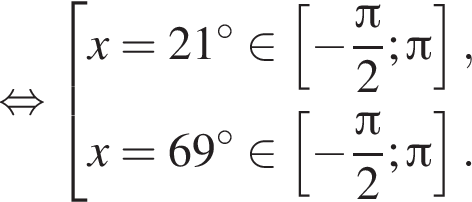
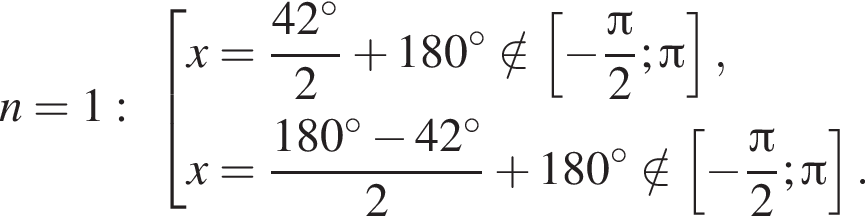
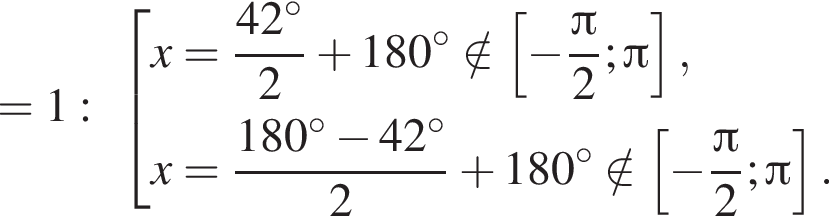
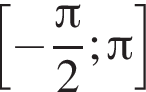 2 корня.
2 корня.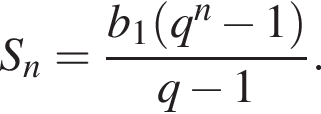 Выразим первый член:
Выразим первый член: 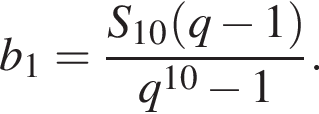 Вспомним, что
Вспомним, что 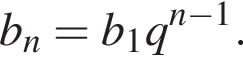
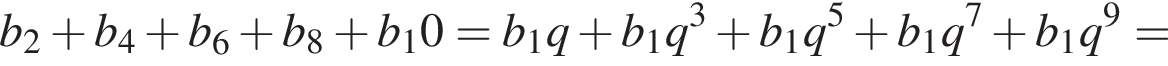
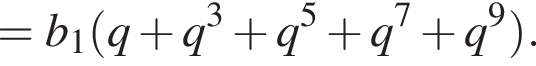
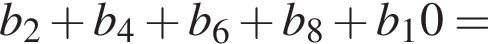
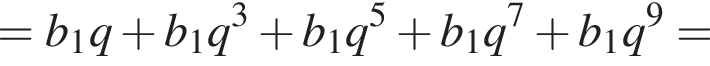
 и знаменателем
и знаменателем 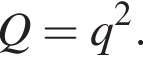 Тогда
Тогда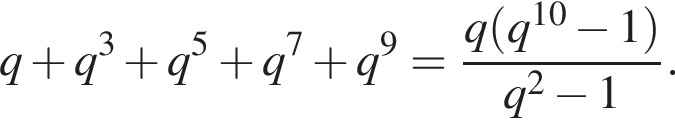
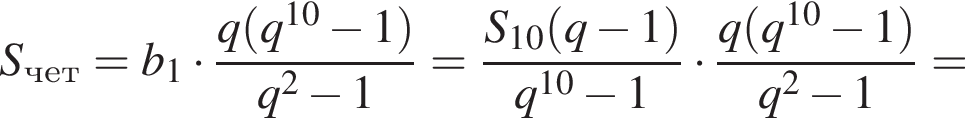
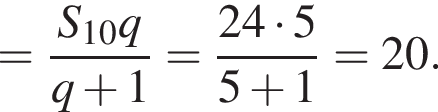
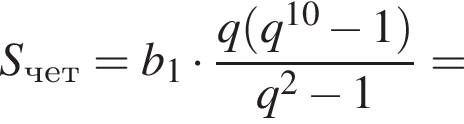
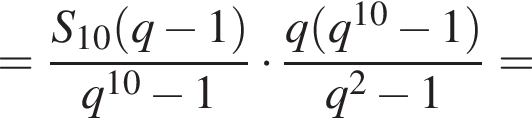

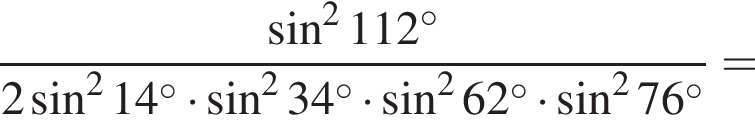
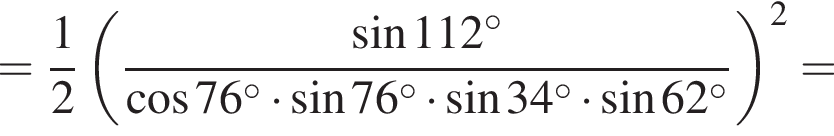
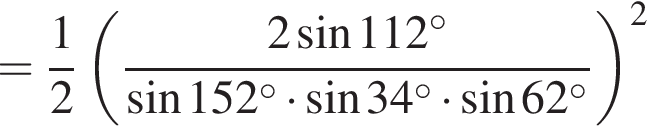
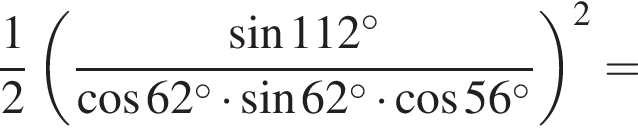
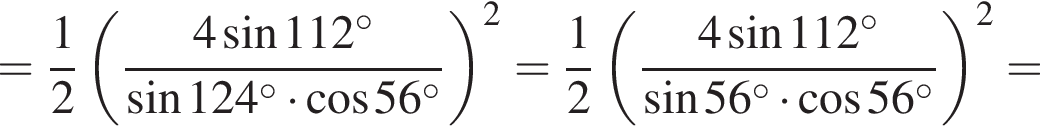
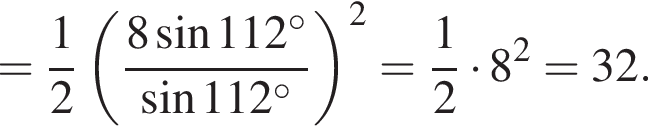
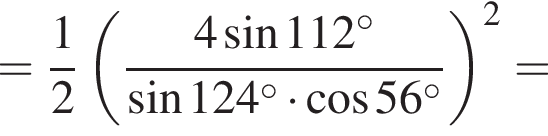
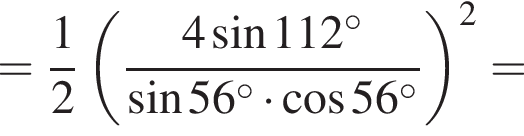
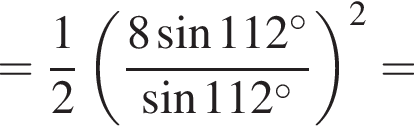
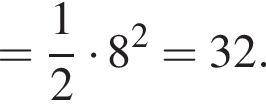
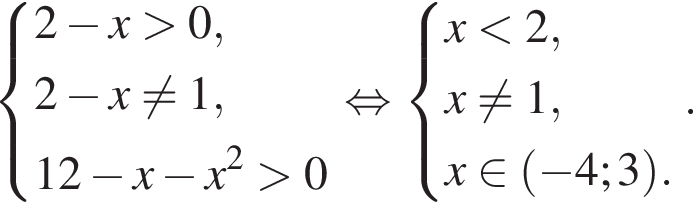
 Их сумма:
Их сумма: 
 имеем:
имеем: 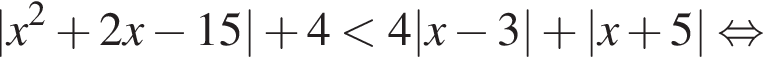
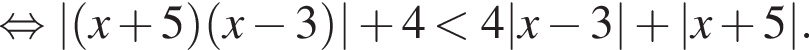
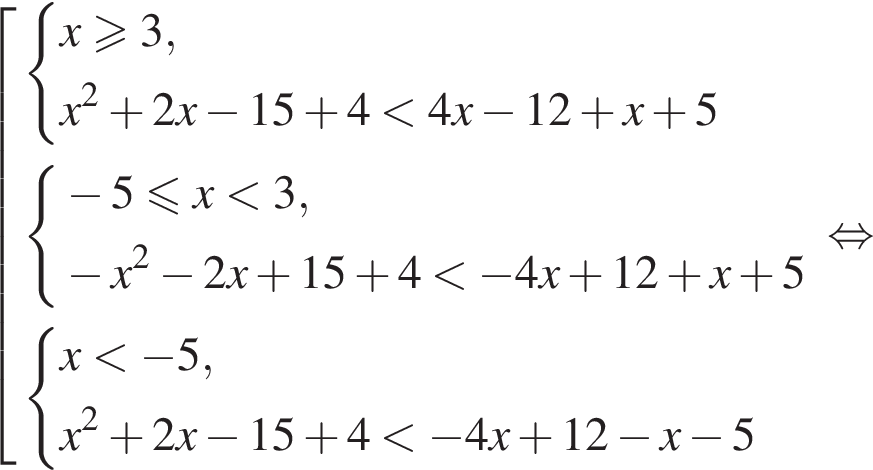
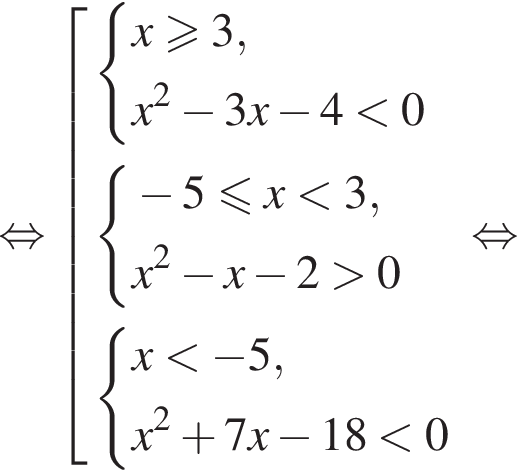
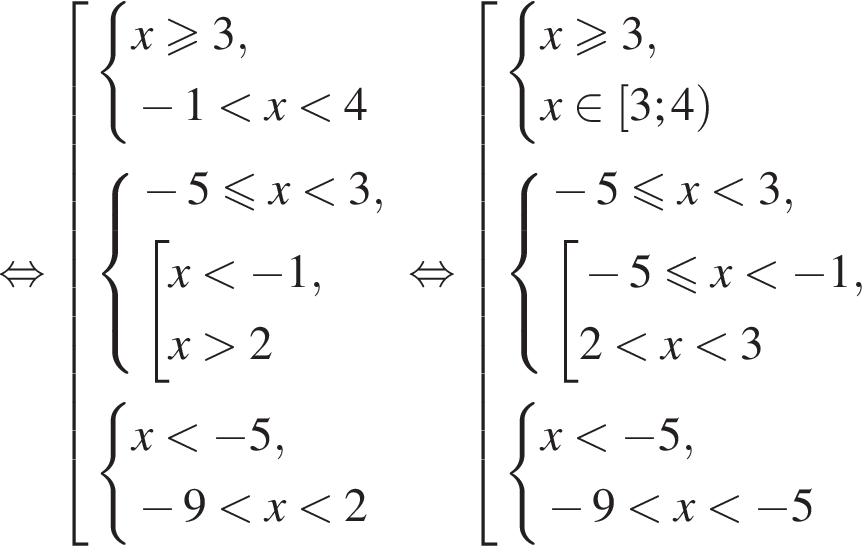
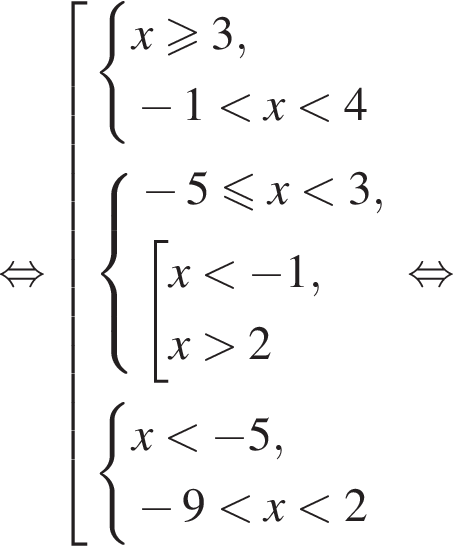
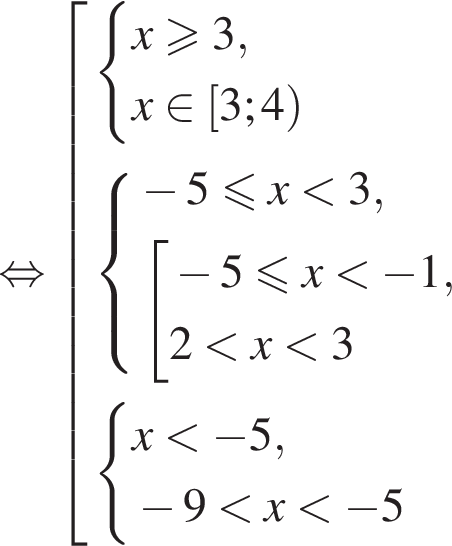
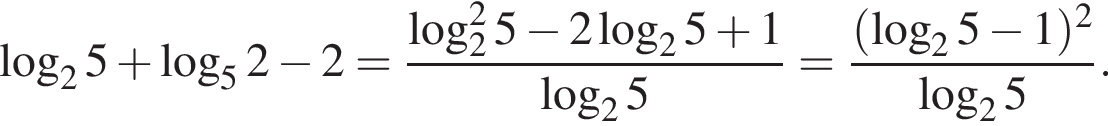
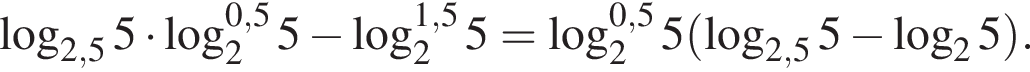
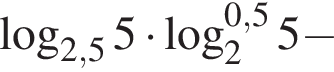
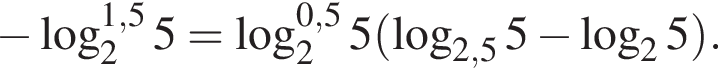
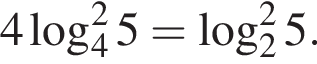 Тогда имеем:
Тогда имеем: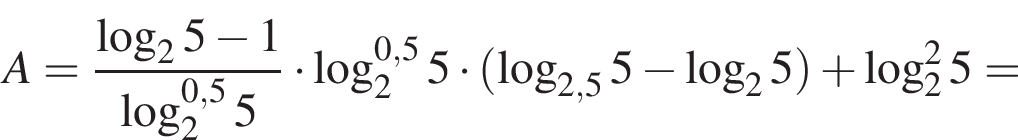
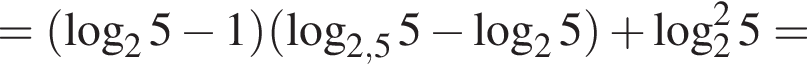
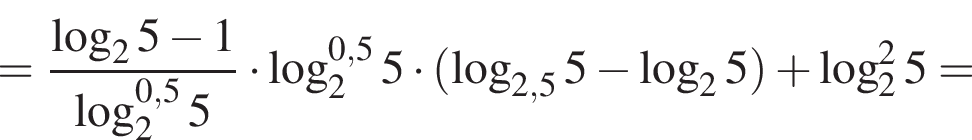
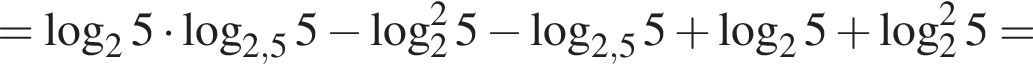
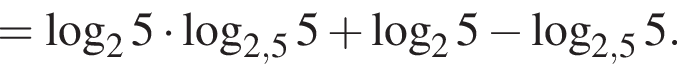
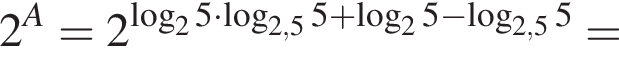
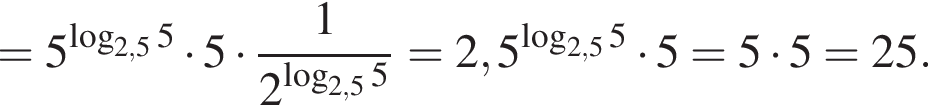
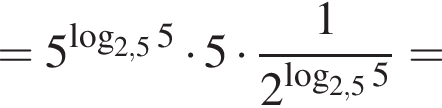
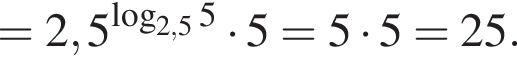
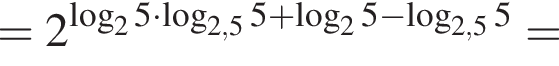
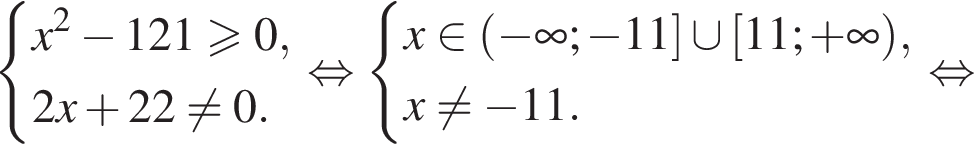
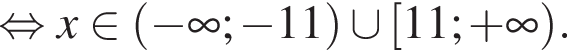
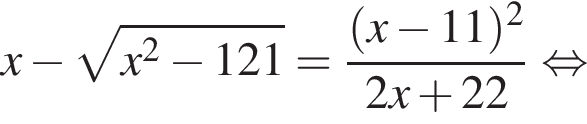
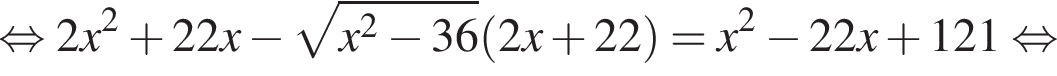
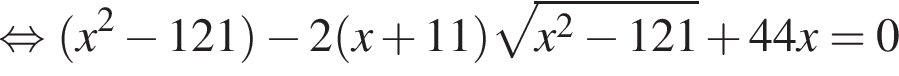
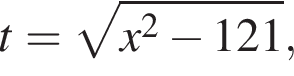 тогда
тогда 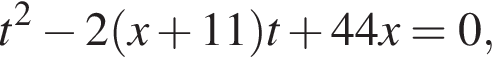 откуда
откуда 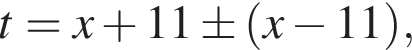 то есть
то есть